[Algorithm/JS] 백준 3053번 택시 기하학

🔗 문제 바로가기 (opens new window)

Question

19세기 독일 수학자 헤르만 민코프스키는 비유클리드 기하학 중 택시 기하학을 고안했다.

택시 기하학에서 두 점 T1(x1,y1), T2(x2,y2) 사이의 거리는 다음과 같이 구할 수 있다.

D(T1,T2) = |x1-x2| + |y1-y2|

두 점 사이의 거리를 제외한 나머지 정의는 유클리드 기하학에서의 정의와 같다.

따라서 택시 기하학에서 원의 정의는 유클리드 기하학에서 원의 정의와 같다.

원: 평면 상의 어떤 점에서 거리가 일정한 점들의 집합

반지름 R이 주어졌을 때, 유클리드 기하학에서 원의 넓이와, 택시 기하학에서 원의 넓이를 구하는 프로그램을 작성하시오.

Input

첫째 줄에 반지름 R이 주어진다. R은 10,000보다 작거나 같은 자연수이다.

Output

첫째 줄에는 유클리드 기하학에서 반지름이 R인 원의 넓이를, 둘째 줄에는 택시 기하학에서 반지름이 R인 원의 넓이를 출력한다. 정답과의 오차는 0.0001까지 허용한다.

Input 1

1

Output 1

3.141593
2.000000

---

Input 2

3.141593
2.000000

Output 2

21

---

Input 3

1385.442360
882.000000

Input 2

42

Output 3

5541.769441
3528.000000

Solution

const input = require('fs').readFileSync('dev/stdin').toString().trim();
const R = Number(input);
console.log((Math.pow(R, 2) * Math.PI).toFixed(6));
console.log((Math.pow(R, 2) * 2).toFixed(6));

유클리드 기하학과 택시 기하학은 난생 처음 들어보는 기법이었다.

문제만 봐서는 무슨 말인지 알 수 없어서 먼저 유클리드와 택시 기하학에 대해서 알아보았다.

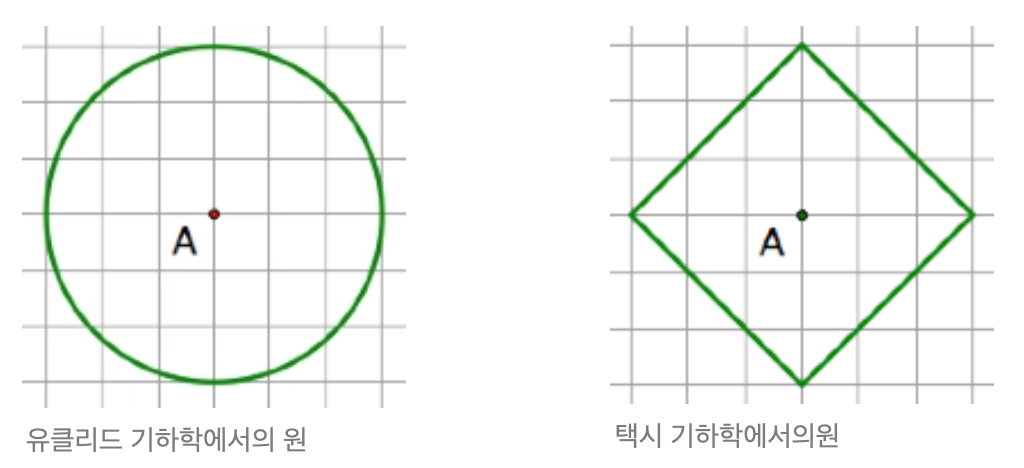
위 이미지와 유클리드와 택시 기하학에 대한 내용은 이 글 (opens new window)을 참고했고,

위 이미지에서 힌트를 얻었다. 유클리드 기하학과 의 지름과 택시 기하학의 대각선 길이는 같다는 것을 알 수 있다.

때문에 유클리드 기하학 을 통한 원의 넓이는 원주율을 공식으로 구할 수 있었고,

택시 기하학 원은 마름모 넓이 공식을 통해 구할 수 있었다.

유클리드 가하학 원의 넓이 = 반지름^2 _ 원주율
택시 기하학 원의 넓이 = 반지름^2 _ 2

따라서 제곱 연산을 하는 메소드 Math.pow 와 원주율 Math.PI 를 활용할 수 있으며

여섯번째 소수점까지 구하기 위해 toFixed(6) 메소드를 사용했다.

유클리드 기하학에서 원의 넓이 = (Math.pow(R, 2) * Math.PI).toFixed(6)
택시 기하학에서 원의 넓이 = ((Math.pow(R, 2) * 2).toFixed(6)